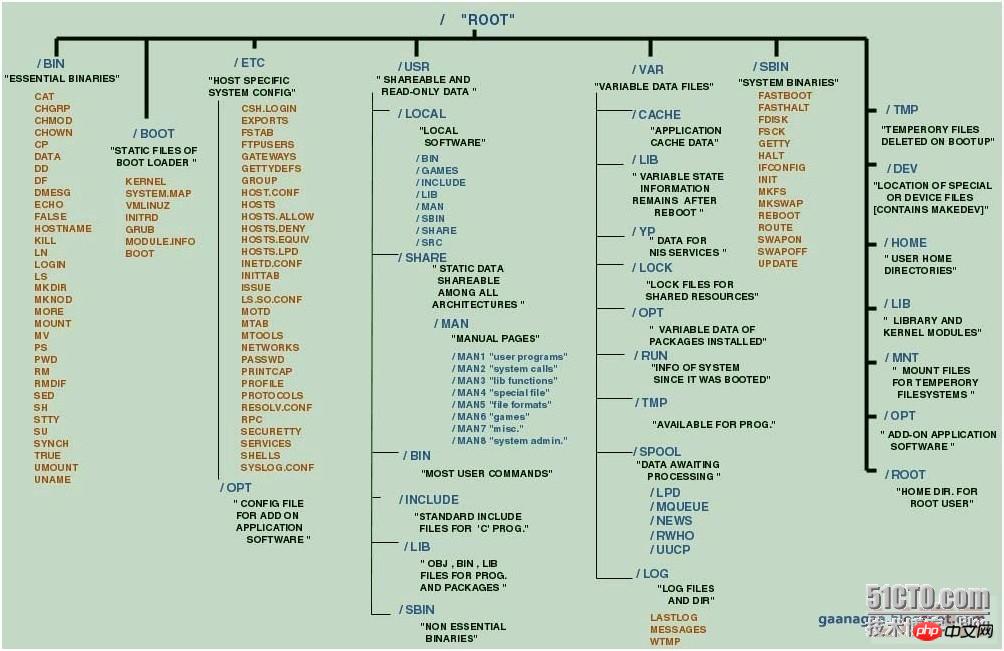
centos如何进救援模式

centos如何进救援模式？

1.右击虚拟机，选择电源—打开电源时进入Bios，进入Bios

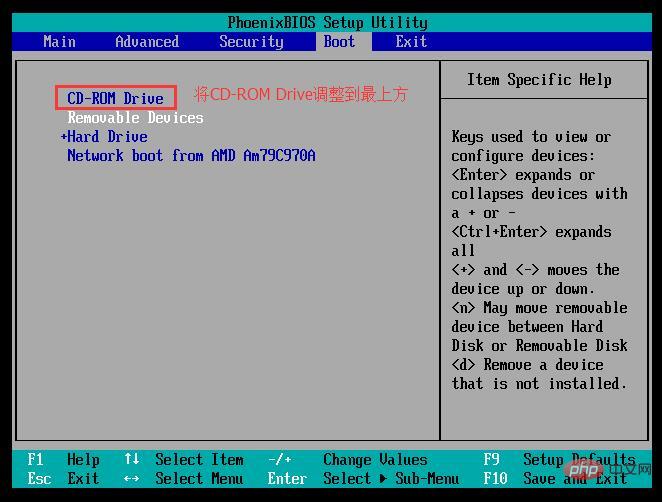
2.进入Bios后，将Boot下的CD-ROM Drive移到最上面，然后按F10键保存重启

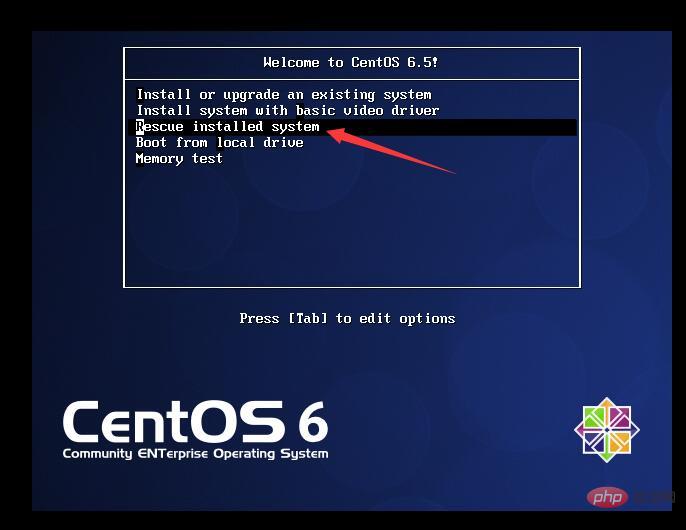
3.重启后进入Menu，选择Rescue installed system，回车

4.启动救援模式中，会弹出多个对话框进行选择，语言默认使用en，键盘使用默认的us，挂载选项直接continue，后面就一直OK，最后选择shell，然后就进入了救援模式

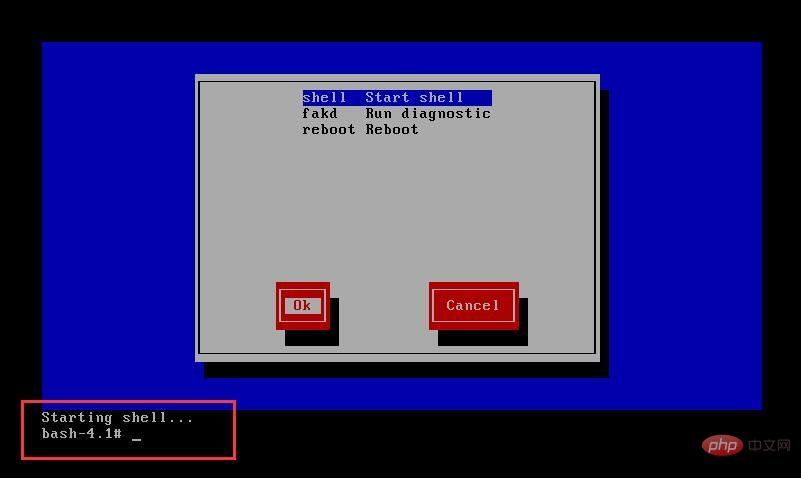
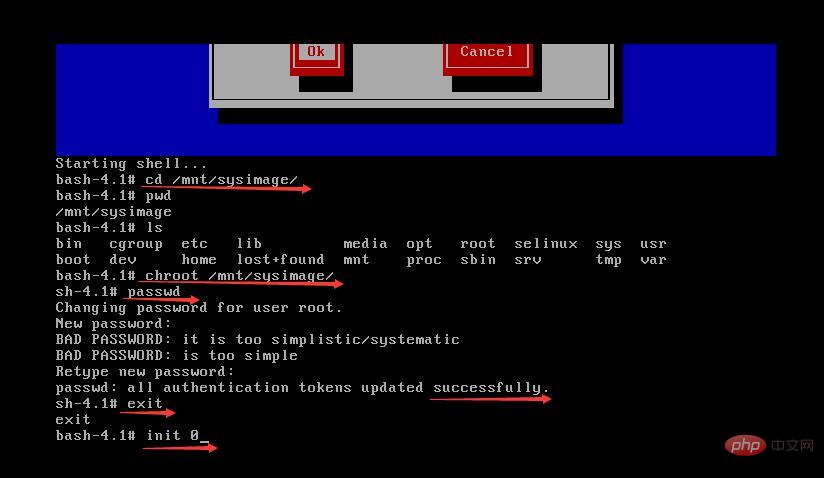
5.进入到挂载分区cd /mnt/sysimage/，切换bash为shchroot /mnt/sysimage，然后执行passwd进行更改密码，再exit退出到rescue系统中，最后reboot重启；注意： 密码更改完成重启后，还要关机更改Bios中，把CD-ROM Drive的顺序改回去，不然每次启动系统都会进入Menu

相关参考：centos教程

以上就是