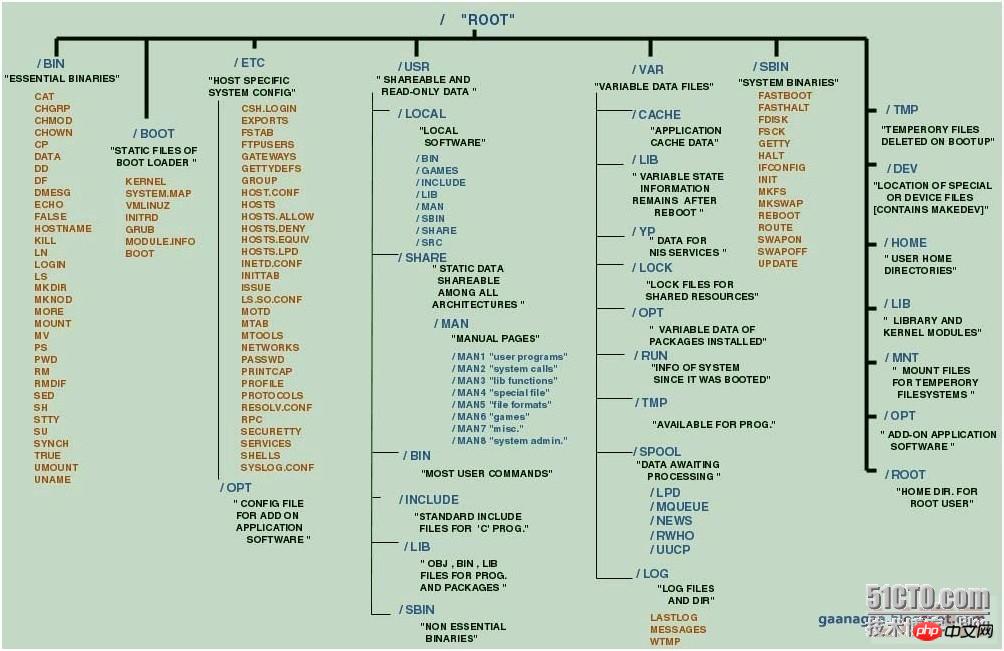
1、lsb_release -a,即可列出所有版本信息
[root@S-CentOS ~]# lsb_release -a LSB Version: :base-4.0-amd64:base-4.0-noarch:core-4.0-amd64:core-4.0-noarch:graphics-4.0-amd64:graphics-4.0-noarch:printing-4.0-amd64:printing-4.0-noarch Distributor ID: CentOS Description: CentOS release 6.5 (Final) Release: 6.5 Codename: Final
这个命令适用于所有的linux发行版,包括RedHat、SUSE、debian…等发行版。
2、cat /etc/redhat-release,这种方法只适合Redhat系的Linux
[root@S-CentOS home]# cat /etc/redhat-release CentOS release 6.5 (Final)
3、cat /etc/issue,此命令也适用于所有的Linux发行版
[root@S-CentOS home]# cat /etc/issue CentOS release 6.5 (Final) Kernel r on an m
推荐教程:linux教程
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
喜欢就支持一下吧
相关推荐