
1、编辑/etc/php.ini配置文件
vim /etc/php.ini

2、修改错误提示范围
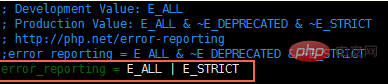
3、开启错误提示
立即学习“PHP免费学习笔记(深入)”;

4、添加读写权限,重启相关服务
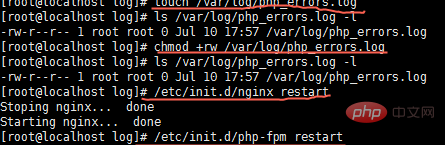
推荐教程:centos教程
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
喜欢就支持一下吧
相关推荐


1、编辑/etc/php.ini配置文件
vim /etc/php.ini

2、修改错误提示范围

3、开启错误提示
立即学习“PHP免费学习笔记(深入)”;

4、添加读写权限,重启相关服务

推荐教程:centos教程