本文在介绍系统自动创建的默认安全组和自己创建的安全组的默认规则的基础上,重点探讨了其具体步骤。
安全组默认规则
本文介绍系统自动创建的默认安全组和您自己创建的安全组的默认规则。
说明
安全组是有状态的。如果数据包在出方向(Outbound)被允许,那么对应的此连接在入方向(Inbound)也被允许。更多安全组相关的概念,请参见 安全组。
系统自动创建的默认安全组
在一个地域创建ECS实例时,如果当前账号在这个地域里尚未 创建安全组,您可以选择系统自动创建的默认安全组,如下图所示。

默认安全组中的默认规则仅设置针对ICMP协义、ssh 22端口、RDP 3389端口、http 80端口和https 443端口的入方向规则。网络类型不同,安全组规则不同。
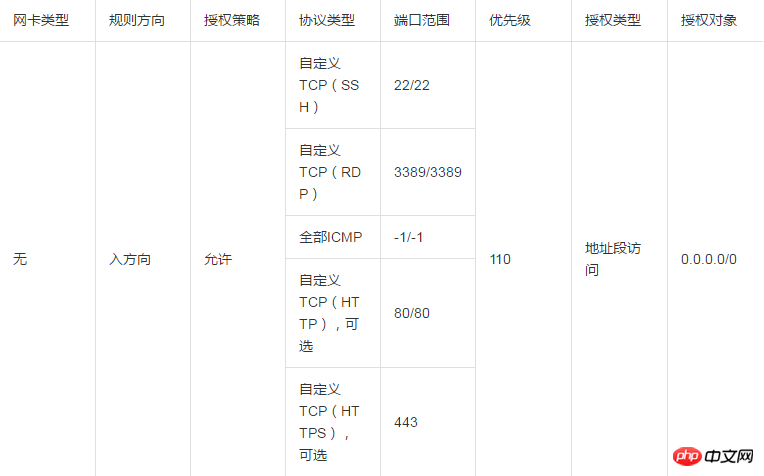
VPC:VPC类型安全组规则不区分内网和公网。VPC类型ECS实例的公网访问通过私网网卡映射完成,所以,您在实例内部看不到公网网卡,在安全组里也只能设置内网规则。安全组规则同时对内网和公网生效。VPC类型默认安全组的默认规则如下表所示。
经典网络默认安全组的默认规则如下表所示。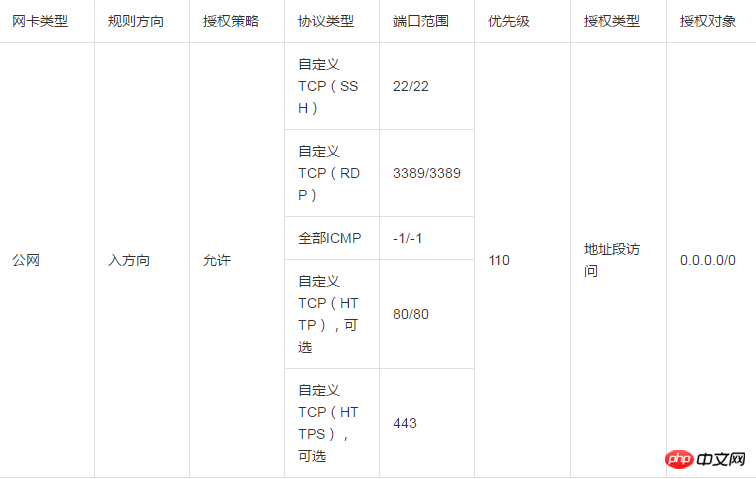
说明
默认安全组规则的优先级为110,表示默认规则的优先级永远比您手动添加的安全组规则低,随时可被覆盖。手动添加安全组规则时,优先级范围为[1, 100]。关于安全组规则优先级的信息,请参见 ECS安全组规则优先级说明。
根据业务需要,您可以在默认安全组中 添加安全组规则。
自己创建的安全组
创建安全组 后,未添加任何安全组规则之前,内网和公网默认规则如下:
出方向: 允许所有访问。
入方向: 拒绝所有访问。
如果您的实例在这样一个全新的安全组中,您只能 使用管理终端连接 ECS 实例,但是不能通过远程连接软件登录实例,无论是 使用用户名密码验证连接 linux 实例 还是 使用软件连接windows实例。
根据业务需要,您可以在自建的安全组中 添加安全组规则。