为什么用了https,仍然被流量劫持?
您好,我是 chrome 浏览器公司的小雪,最近我们访问千度网、淘贝网的网页中时常出现不少奇怪的广告,一直被投诉,听领导说 361 杀毒公司的周老师是这方面的专家,想请您帮忙诊断一下,到底这些广告是怎么来的
老周,有人找你,一大早,361 杀毒公司的老周就被吵醒。今天的阳光很明媚,老周伸了伸懒腰,这才踱步走向工作室。

图片来自 Pexels
1、广告再临
“是谁一大早的就来吵吵,坏了我的瞌睡”,听得出来,老周有点不太高兴。
“咚咚~”,老周微微抬头一瞥,只见一甜美女子出现在工作室的门前。
推荐:《web服务器安全教程》

老周一下从座椅上弹了起来,三步并作两步,走到女子面前,作出欢迎的手势:“美女请进”。
二人坐罢,老周扶了下镜框,又整理了一下格子衬衣,一副温文尔雅的作态,轻声问到:“不知美女到访,所为何事?”
女子倒是一副焦急的样子,“您好,我是 Chrome 浏览器公司的小雪,最近我们访问千度网、淘贝网的网页中时常出现不少奇怪的广告,一直被投诉,听领导说 361 杀毒公司的周老师是这方面的专家,想请您帮忙诊断一下,到底这些广告是怎么来的”!
老周听得有些不好意思,连连挥手,“原来是小雪姑娘,哪里哪里,勇斗病毒木马,消灭流氓软件本就是我 361 公司的分内之事,在下也只是尽一些绵薄之力罢了”。
“周老师别谦虚了,您之前揪出 IE 公司的木马入侵的事迹已经传遍整个 windows 帝国了,大家都知道您的厉害。这一次广告的问题,就拜托了”,小雪看着老周,仿佛眼里闪着星星。
“别客气,这事儿包在我身上了”,小雪起身,连说了几句谢谢就离开了。
2、谁动了 https 流量
此刻,负责网络数据过滤的大白正在忙碌着,突然一只手搭在了他的肩膀上,大白回头一看,正是老周。
“老周,什么风把你吹到这里来了,你不在安全实验室分析恶意代码,跑我们网络部门来干嘛?”
老周拍了下大白的肩膀,说到:“大白啊,有点事想请你帮帮忙,你帮我瞅瞅,Chrome 浏览器的流量中是不是被插入广告了?”
“就这事啊,前段时间发现路由器老给插入广告,我就给做了特征屏蔽,原以为它们消停了,这才没几天又卷土重来了?”,大白说完调出了 Chrome 公司的流量,准备一看究竟。
大白越看眉头锁的越紧,“应该没有吧,我看访问千度网和淘贝网都是用的 HTTPS 协议,按理说路由器没有可能插入广告了啊!”
“HTTPS 协议?为什么用这个就没法插入广告?”,老周问到。
“这都不知道啊,你这 361 公司安全实验室领导怎么当上去的啊”,大白一脸无语的表情。

老周有点难为情,“唉,老弟你也别取笑我了,这个术业有专攻嘛,我擅长病毒木马代码的分析,对网络协议这块确实知之甚少,劳烦大白老弟给说道说道”。
大白似乎是感觉自己的话说的有些重了,也借坡下坎,“老周啊,刚才我跟你开玩笑的,你可别往心里去啊”。
“没事没事,你快给我说说这 HTTPS 协议,帮助我早点破案吧!”
“好嘞,你稍等啊”,说完,大白开始在白板上画了起来。
3、什么是 HTTPS
“HTTPS=HTTP+ssl/TLS,这门技术,说简单也简单,说复杂也复杂。简单来说,就是为了网络数据的安全性,通过加密传输的方式来对传统上网的 HTTP 流量进行保护”,大白一边画着图一边给老周讲述。

“明白,那么问题来了,用什么加解密算法呢?对方如何知道用什么算法以及用什么密钥解密呢?”,老周一下抓到了关键点。
“唉,问到点子上了。在正式传输数据之前,双方会有一个协商过程,为后面所选择的加密算法,以及要使用的密钥达成一致。”
“那么问题又来了,这个协商的内容要是被别人知道了,他不就可以按图索骥,解密传输的内容了吗?”,老周的反应很快。
“老周果然是老周!加密算法被知道是无所谓了,毕竟算法都是公开的,关键在于这个用于后续加密的密钥,这个才是需要保护的关键,这个不能让别人知道”,说罢,大白又继续画起来。

“so?怎么保护这个密钥呢?你倒是说啊”,老周有点着急了。
“注意哦,高能来了,双方使用一个叫非对称加密的方式来传输…”
“等一下”,老周打断了大白,“非对称加密,这是个什么意思?”
大白默默叹了一口气,“常见的加密方式叫对称加密算法,所谓对称,就是加密和解密使用同一个密钥。那与此相对的,非对称加密,就是说加密和解密使用的是不同的密钥,明白了吧”!
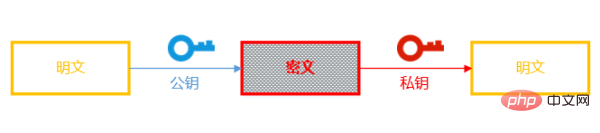
老周略微思索,点了点头,“我知道了,你继续刚才说的,怎么用这个非对称加密算法来传输后面需要的密钥呢!”
大白继续说到:“客户端产生一个随机数,使用公钥加密,发给服务端,服务端使用私钥解密取得这个随机数,再根据这个随机数和其他信息计算出一个 key,就作为后续加密内容使用的密钥了!”
“等等,客户端的公钥是哪里来的?”
“最开始的时候,客户端发来请求,服务端在响应中,会把公钥告诉客户端。好了,我画完了,整个过程就是这样的。”
大白放下画笔,一副完整的 HTTPS 协议握手过程图浮现了出来:
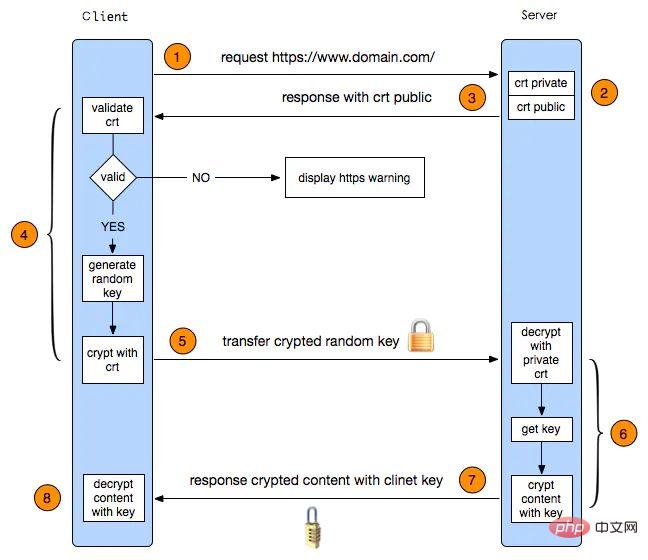
老周反复端详,许久总算开口:“过程我倒是看懂了,不过我总感觉这不多此一举吗,直接使用非对称加密算法不就得了,这么折腾!”
大白连连挥手,“你想的倒是简单,非对称加解密算法执行起来麻烦的多,耗费的时间会多很多倍,如果全程使用非对称加密算法,那将会严重影响上网体验。算法是个好算法,但用的代价也很大,所以权衡之下,好钢用在刀刃上,就只用来传输密钥,后面的正式数据传输,还是用常规的对称加密算法,来的经济划算。”
老周点了点头,一会儿低头思考,一会儿又抬头看着流程图。
又过了许久,老周指着流程图,再次提问:“我说大白,如果我在客户端和服务端之间插入一个角色,对客户端冒充服务端,对服务端又冒充客户端,就能从中作梗,修改数据包,插入广告了是吧?”
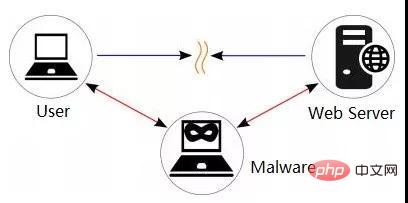
正在喝水的大白听后呛得连连咳嗽,“你说的就是中间人攻击嘛!你当 HTTPS 是玩具嘛,这么容易就被劫持,笑话!注意看图,那里有个认证环节,不是谁都能冒充的!”
老周又看了看图,“怎么认证法,我倒是听听!”
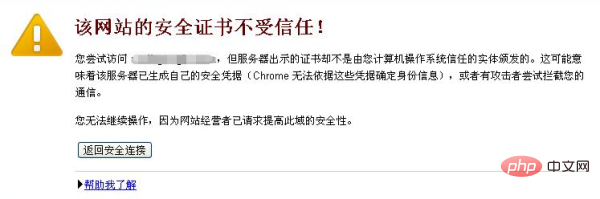
“在服务端的响应中,我前面说的公钥是在一个叫证书的东西里面,这个证书就是用来标识服务端的身份的,是由权威机构颁发的,客户端收到证书后,会检查是否是可信任的,如果不受信任就会及时中止后面的流程。”
“那如何判断一个证书是可信任的呢?”
“帝国早已把受信任的证书安装好了,届时只需调用 API 查一下即可!”
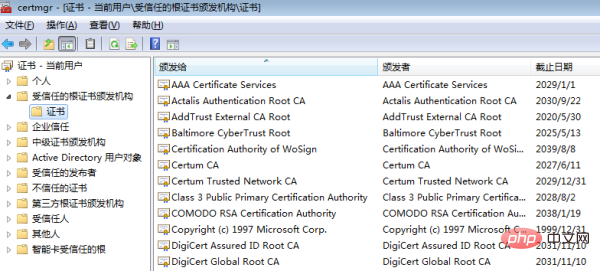
老周思来想去,总觉得哪里有问题,却又说不上来。
4、真相只有一个
一连过了几天,老周依旧毫无头绪,这事儿就这样搁置了。
福无双至,祸不单行。这案子还没弄明白,firefox 公司又出事了。
原来,361 杀毒公司检测到 Firefox 秘密启动了有木马特征的进程,老周再一次带队前往勘查,Firefox 公司的小狐负责对接此事。
老周来到了 Firefox 磁盘存储目录,打算先排查一下木马文件是什么来头。

“这是一堆什么数据?”,老周指着一堆文件问到。
“周老师,这是网页缓存数据”,一旁的小狐回答。
“打开看看,能否找到一些攻击痕迹?”
老周环顾四周,指着另一堆文件问到:“这又是一堆什么数据?”
“周老师,这是一堆证书信息,HTTPS 握手时认证服务器所用的,跟这次攻击事件应该没关系的”,小狐继续解释到。
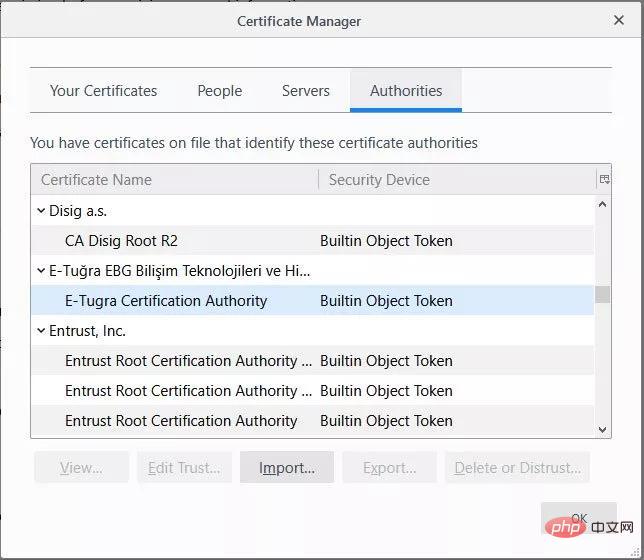
“认证用?帝国不是存储了受信认的证书吗,你们还保存证书信息做什么?”,老周有些不解。
“帝国存储的受信任证书我们可不认,谁知道那里面都是些什么证书,太不可靠了,我们 Firefox 浏览器公司自己做认证,不用那一套”,小狐言语之间流露着些许得意。
听完小狐的回答,老周突然愣住了,短暂的几 ms 之后反应了过来,掏出了从 Chrome 公司拿来的千度网证书,打算请小狐看一下。
小狐接过证书,仔细察看,片刻之后一口咬定的说:“这证书有问题!”
老周眼前闪过一道亮光,追问到:“哪里有问题?”

“这证书颁发机构叫 ABSafe,不在我们受信任的列表中!再说了,我这里有缓存千度网的证书,根本不是这样的,这肯定是假的,你看!”
老周拿着两个证书反复查看,不时点点头,之前困扰多时的问题终于有了答案。
“我明白了,真相只有一个!一定是有人把这个 ABSafe 颁发机构安装到了帝国受信任列表,以此骗过了 Chrome 公司!进行了 HTTPS 中间人劫持!YES!”,老周说完用力挥了挥拳头。
“周老师,您在说什么啊,我怎么听不懂?”,看着老周自言自语,小狐满脸的问号。
老周叮嘱同行的老齐继续勘察,匆忙拜别小狐就离开了。

这天夜里,两个黑影出现在了帝国受信任根证书仓库。
“原来是有人把我们安装的根证书给删掉了,难怪刚才 Chrome 浏览器访问千度网报了警告”,其中一个胖的黑影说到。
瘦的黑影捂住了胖子的嘴巴,“嘘,你给我把着点风,我去重新装上!”
瘦的黑影蹑手蹑脚走了过去,从怀里掏出了一个东西。

“别动!安全检查!”,突然一束光线射了过来,原来老周带着队伍在此潜伏多时了。
“竟然是你们,禁广大师!千度网和淘贝网的广告也是你们加的是吧?”,老周大声质问。
胖瘦黑影面面相觑,老实交代了一切。
彩蛋:“老齐,Firefox 公司的案子有什么发现吗”,“老周,你还是再来一趟吧,情况有点复杂”。欲知后事如何,请关注后续精彩…
更多安全、web服务器安全教程知识,请关注php中文网!
本文转载自:https://netsecurity.51cto.com/art/202002/610987.htm


















