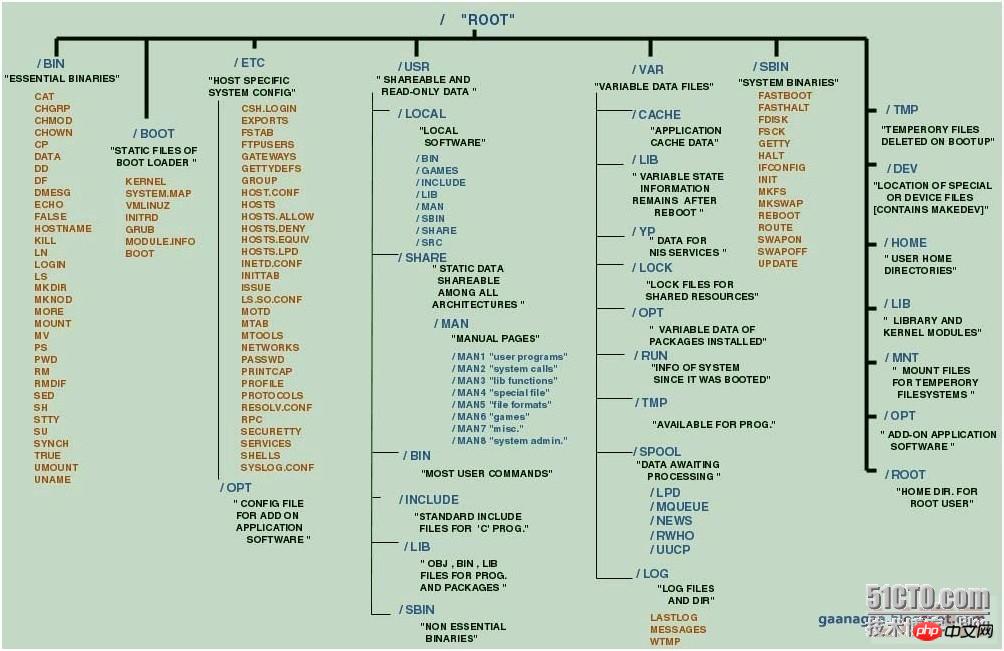
比如说要修改host文件
首先使用vi /etc/hosts命令打开hosts文件的阅读模式,按o键可进入编辑模式,并在当前位置的后面插入一行。
录入内容后,按Esc键退出编辑模式并进入阅读模式。
命令:w保存文件;
命令:q退出。
相关视频学习教程推荐:linux视频教程
编辑模式命令:
i :在当前位置插入
a:在当前位置后追加
o:在当前位置的后面插入一行
I :在行头插入
A:在行尾追加
O:在当前位置的前面插入一行
阅读模式命令:
:w 保存文件
:w filename 保存成filename文件
:q 退出
:q! 强行退出
:w! 强行写
:wq 保存退出
😡 同wq
相关文章教程推荐:linux视频教程
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
喜欢就支持一下吧
相关推荐