一个链接查 QQ 好友 IP 地址,GPS 定位,摄像头图片。带自动邮箱提醒。——无引流,求管理员通过。
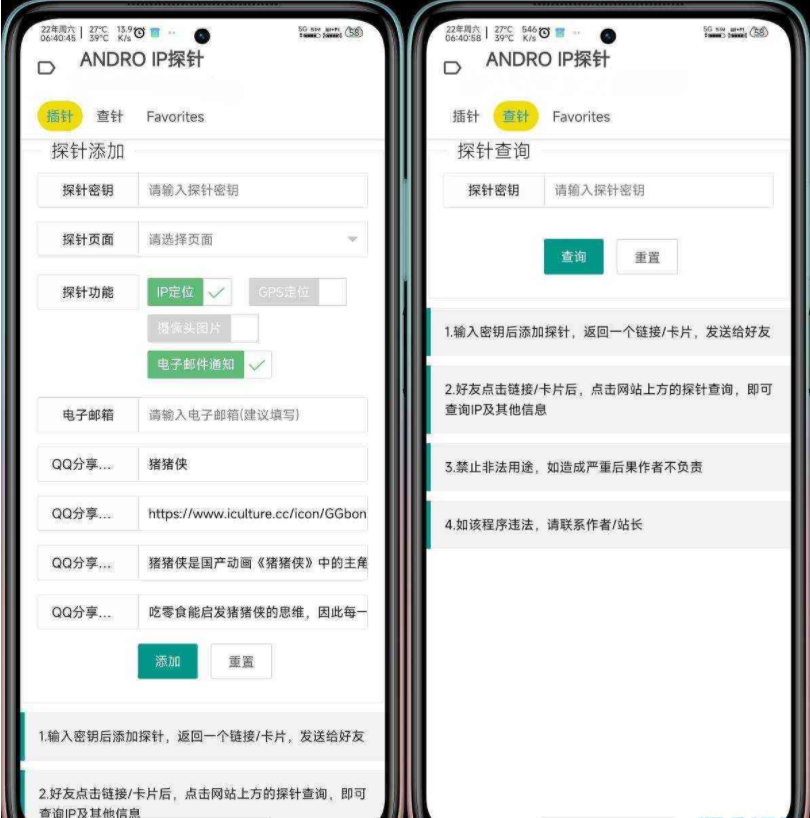
使用教程: 输入秘钥,最好是复杂一点,不能跟别人重复,然后输入提醒的邮箱,
就可以生成链接,有人访问那个链接就会游戏提醒详细信息,也可以用秘钥查询。
下载地址:
密码:1jbo
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END

一个链接查 QQ 好友 IP 地址,GPS 定位,摄像头图片。带自动邮箱提醒。——无引流,求管理员通过。
使用教程: 输入秘钥,最好是复杂一点,不能跟别人重复,然后输入提醒的邮箱,
就可以生成链接,有人访问那个链接就会游戏提醒详细信息,也可以用秘钥查询。

下载地址:
密码:1jbo